Задача 3.1
Частица находится в двумерной прямоугольной потенциальной
яме с бесконечно высокими стенками. Координаты
![]() и
и ![]() частицы лежат в
пределах
частицы лежат в
пределах ![]() ,
, ![]() , где
, где ![]() и
и ![]() - стороны ямы.
Определите вероятность нахождения частицы с наименьшей энергией в области:
а)
- стороны ямы.
Определите вероятность нахождения частицы с наименьшей энергией в области:
а) ![]()
![]() ; б)
; б) ![]()
![]() ; в)
; в) ![]() ,
, ![]()
![]() . Убедитесь, что
. Убедитесь, что ![]() .
.
Решение:
Двумерная потенциальная яма имеет вид, представленный на рисунке 1:

![]()
![]()
![]()
Рисунок 1
Составим уравнение Шредингера для области ![]() :
:
![]()
![]() (1)
(1)
Запишем уравнение Шредингера в виде:
![]() (2)
(2)
где ![]() .
.
Решение этого дифференциального уравнения имеет вид:
![]() (3)
(3)
Воспользуемся граничными условиями, которые накладываются на волновую функцию.
Из условия непрерывности следует:
![]()
![]() (4)
(4)
Учитывая (3) и (4), что волновая функция примет вид:
![]() (5)
(5)
Далее из условий непрерывности волновой функции на границе
области ![]() :
:
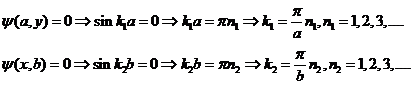 (6)
(6)
Следовательно, волновая функция будет иметь вид:
![]() (7)
(7)
Найдём частные производные второго порядка ![]() и
и ![]() от пси-функции
от пси-функции ![]() :
:
 (8)
(8)
Подставим полученные выражения для ![]() и
и ![]() в
уравнение Шредингера (2) и получим:
в
уравнение Шредингера (2) и получим:
![]() (9)
(9)
Так как ![]() , то определим из уравнения (9) энергетический спектр
частицы:
, то определим из уравнения (9) энергетический спектр
частицы:
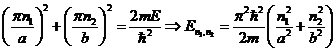 (10)
(10)
где ![]() - квантовые числа. Из
выражения (10) следует, что энергетический спектр частицы является дискретным,
и наименьшее значение энергии соответствует значениям квантовых чисел
- квантовые числа. Из
выражения (10) следует, что энергетический спектр частицы является дискретным,
и наименьшее значение энергии соответствует значениям квантовых чисел ![]() :
:
![]() (11)
(11)
Соответствующая этому состоянию волновая функция имеет вид:
![]() (12)
(12)
Используя условие нормировки волновой функции
найдём коэффициент ![]() :
:
![]() (13)
(13)
Таким образом, волновая функция ![]() имеет следующий вид:
имеет следующий вид:
![]() (14)
(14)
Квадрат модуля волновой функции определяет плотность вероятности нахождения частицы. Найдём функцию плотности вероятности нахождения частицы, находящейся в состоянии, описываемом волновой функцией (14):
![]() (15)
(15)
Графически функция плотности вероятности - рисунок 2:
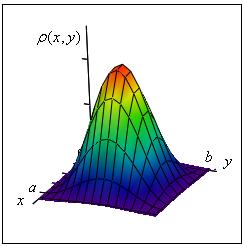
Рисунок 2
Найдём вероятность нахождения частицы в области ![]() :
:
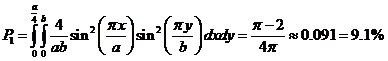 (16)
(16)
Найдём вероятность нахождения частицы в области ![]() :
:
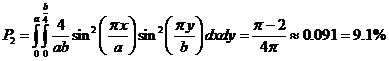 (17)
(17)
Найдём вероятность нахождения частицы в области ![]() ,
, ![]() :
:
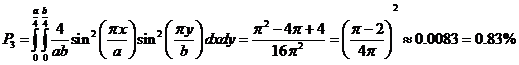 (18)
(18)
Из (18) следует, что ![]() .
.
Ответ: Вероятности нахождения частицы равняются:
![]() :
: ![]()
![]() :
: ![]()
![]() ,
, ![]() :
: ![]()