Задача № 5.144.
Определить энергию электрона атома водорода в состоянии, для
которого волновая функция имеет вид ![]() , где
, где ![]() ,
, ![]() и
и ![]() - некоторые постоянные.
- некоторые постоянные.
Решение:
Потенциальное поле, в котором находится электрон в атоме водорода, имеет вид:
![]() (1)
(1)
где ![]() . Составим уравнение Шредингера:
. Составим уравнение Шредингера:
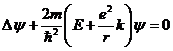 (2)
(2)
Так как волновая функция в нашем случае зависит только от
координаты ![]() , то в нашем случае будем использовать только радиальную
часть оператора Лапласа:
, то в нашем случае будем использовать только радиальную
часть оператора Лапласа:
![]() (3)
(3)
С учётом выражения (3) уравнение Шредингера примет вид:
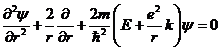 (4)
(4)
Волновая функция электрона в заданном состоянии имеет вид:
![]() (5)
(5)
Найдём её первую и вторую производные по
![]() :
:
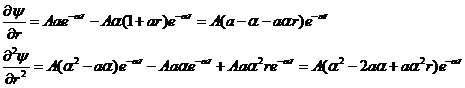 (6)
(6)
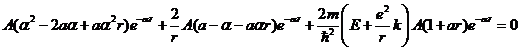 (7)
(7)
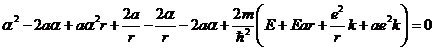
![]() (8)
(8)
Уравнение (8) должно выполняться для любых значений ![]() , поэтому:
, поэтому:
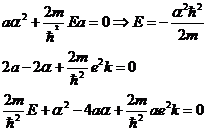 (9)
(9)
Из первого уравнения (9) выражение для энергии электрона подставим в последнее уравнение и получим:
![]()
Из этого уравнения найдём ![]() :
:
![]() (10)
(10)
Подставим (10) в выражение для энергии электрона, найденное из первого уравнения (9) и определим значение энергии электрона в данном состоянии:
![]() (11)
(11)
Что соответствует значению энергии при
![]() , то есть второй энергетический
уровень электрона в атоме водорода.
, то есть второй энергетический
уровень электрона в атоме водорода.
Ответ: ![]() , второй энергетический уровень
, второй энергетический уровень ![]() .
.