Задача № 5.143.
Электрон атома водорода находится в состоянии, описываемом
волновой функцией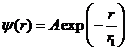 
, где 
и 
- некоторые
постоянные. Найти значения:
а) нормировочного коэффициента ;
б) энергии 
электрона и 
(с помощью уравнения
Шредингера).
Решение:
Постоянную определим из условия
нормировки волновых функций:
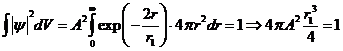(1)
Отсюда получим, что нормировочный коэффициент равняется:
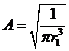(2)
Тогда волновая функция примет вид:
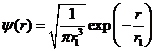(3)
Электрон в атоме водорода находится в потенциальном поле ядра, которое имеет вид:
(4)
где 
. Уравнение Шредингера в нашем случае имеет вид:
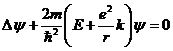(5)
где 
- радиальная
составляющая оператора Лапласа, так как в нашем случае пси-функция зависит
только от координаты . Таким образом, уравнение Шредингера примет вид:
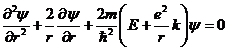(6)
Найдём первую и вторую производную по
от выражения (3):
(7)
(8)
Подставим (3), (7) и (8) в уравнение Шредингера (6) и получим:
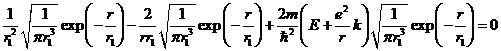(9)
Разделим обе части уравнения (9) на
:
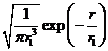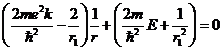(10)
Уравнение (10) должно выполнятся
для любых значений , поэтому:
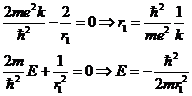(11)
Подставим значение во второе уравнение
(11) и найдём значение энергии частицы в этом состоянии:
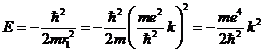(12)
Ответ: а)
значение постоянной в выражении для
пси-функции равняется: ;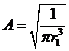
б) постоянная равняется: 
, энергия частицы в данном состоянии: 
.