Задача № 28.

 

Квантовый гармонический осциллятор находится в основном состоянии. Найдите вероятность  обнаружения частицы в области , где  - амплитуда классических колебаний.

 

Решение:

 

Квантовый гармонический осциллятор представляет собой частицу, находящуюся в потенциальном поле вида:

 

                                    (1)

 

График потенциальной энергии изображён на рисунке 1:

 

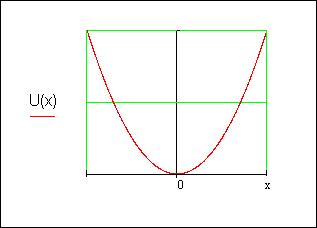
Рисунок 1

В этом случае составляют уравнение Шредингера:

 

                                             (2)

 

Это дифференциальное уравнение имеет решение только при дискретных значениях . Таким образом, энергия квантового гармонического осциллятора квантуется и может принимать следующие значения:

 

                                                                      (3)

 

В основном состоянии квантовое число , поэтому энергия квантового гармонического осциллятора в основном состоянии равна:

 

                               (4)

 

Определим амплитуду классических колебаний:

 

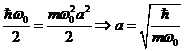                                    (5)

 

Решения дифференциального уравнения (4) имеют вид:

 

                                                     (6)

 

где  - полиномы Чебышева-Эрмита, которые определяются следующим образом:

 

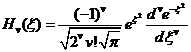                                   (7)

 

                                  

где . Для основного состояния , имеем пси-функцию:

 

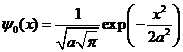                                     (8)

 

Квадрат модуля пси-функции определяет плотность вероятности нахождения частицы:

 

                               (9)

 

Чтобы найти вероятность нахождения частицы в области  нужно проинтегрировать (9) по пределам области:

 

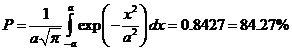                     (10)

 

Ответ:

 

.